Tin Tức

Bán Kính Hội Tụ Và Miền Hội Tụ, Câu 7 Tìm Bán Kính Hội Tụ Miền Hội

Xet Tuyen Trung Cap24/08/2021

0 3.096 4 minutes read

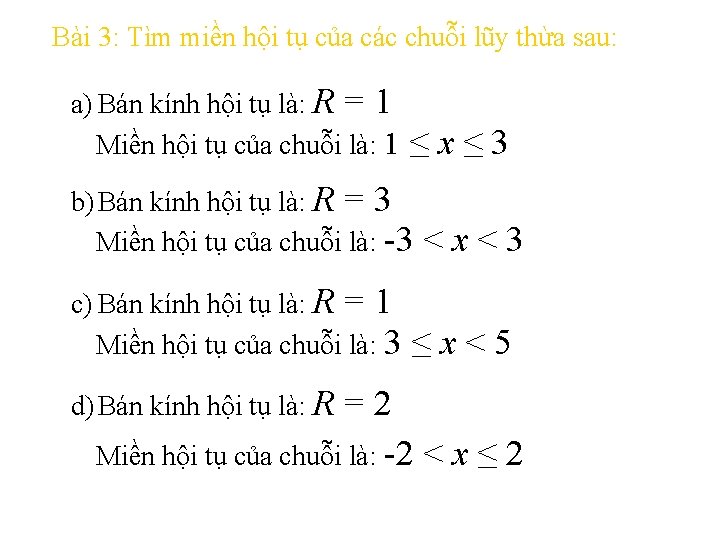
Bán Kính Hội Tụ Và Miền Hội Tụ, Câu 7 Tìm Bán Kính Hội Tụ Miền Hội

+ Khi nào chuỗi (1) hội tụ? Nói rõ hơn ngoài

Có thể bạn quan tâm

chuỗi (1) còn hội tụ tại những điểm

nào khác?

+ Trừ

ra, nếu chuỗi (1) hội tụ thì nó hội tụ đến đâu? Liệu giới hạn đó có phải

Để trả lời câu hỏi đầu, ta quan sát chuỗi lũy thừa một cách độc lập, chưa phải là chuỗi Taylor của hàm nào,

Đang xem: Bán kính hội tụ

Câu hỏi đầu tiên được trả lời qua hai ý sau:

+ (Định lý Abel) Có một số thực không âm

để

– khi

Tại hai đầu mút nói chung ta không biết chuỗi có hội tụ không. Chẳng hạn chuỗi

có bán kính hội tụ

, hội tụ tại

và phân kỳ tại

Vấn đề tại mút các bạn có thể tham khảo thêm ở bài

+ Từ ý trên ta có khái niệm bán kính hội tụ. Vậy bán kính hội tụ được tính như nào?

Bán kính hội tụ được tính nhờ công thức Cauchy-Hardamard

– hoặc

với

– hoặc

với

Lưu ý rằng hai giới hạn trên chưa chắc tồn tại, tuy nhiên vẫn có bán kính hội tụ. Lúc đó bán kính được tính nhờ công thức

với

Các bạn có thể thấy điều này qua ví dụ

có bán kính của chuỗi (2) là

Bán kính cũng có thể bằng

, chẳng hạn khi

Bán kính cũng có thể bằng

, chẳng hạn khi

Khi bán kính hội tụ

0″ class=”latex” /> thì chuỗi (2) hội tụ đều trên

” class=”latex” /> với bất kỳ

Xem Thêm : Logic Mệnh Đề Toán Rời Rạc, Toán Rời Rạc (Discrete Mathematics)

Chuỗi gồm các số hạng là đạo hàm của từng số hạng của chuỗi (2)

cũng có bán kính hội tụ chính là bán kính hội tụ của chuỗi (2) vì

Khi đó chuỗi các đạo hàm cũng hội tụ đều trên

” class=”latex” /> với bất kỳ

. Do đó chuỗi các đạo hàm hội tụ đến đạo hàm của chuỗi (2) tại mọi điểm trong

. Chuỗi (2) hội tụ đến hàm

khả vi trên

Bằng quy nạp sẽ dẫn đến chuỗi (2) hội tụ đến hàm

khả vi vô hạn trên

. Đạo hàm cấp

, của

chính là hàm giới hạn của chuỗi gồm các số hạng là đạo hàm cấp

của số hạng tương ứng trong chuỗi (2). Từ đó có chuỗi (2) là khai triển Taylor của hàm

Giờ ta chuyển sang câu hỏi thứ hai, nghĩa là lúc này chuỗi (2) sinh ra từ việc khai triển Taylor của một hàm khả vi vô hạn

và

Câu hỏi thứ hai trở thành, khi bán kính hội tụ

0″ class=”latex” /> phải chăng

với

Câu hỏi này mới nghe có vẻ không cần thiết lắm nhưng các ví dụ sau chỉ ra sự cần thiết.

Xem thêm: Sinh 2006 Mệnh Gì – Sinh Năm 2006 Mệnh Gì

Ví dụ 1: Hàm

xác định bởi

khi

0″ class=”latex” />

khi

là hàm khả vi vô hạn và đạo hàm mọi cấp của nó tại

đều có giá trị bằng

Ví dụ 2: Hàm

xác định bởi

khi

khi

là hàm khả vi vô hạn và đạo hàm mọi cấp của nó tại

đều có giá trị bằng

Hai ví dụ trên đều có chuỗi Taylor tại

đồng nhất

. Nói cách khác hàm

Xem Thêm : Trung Tâm Sát Hạch Lái Xe Miền Đông Nam Bộ, Trung Tâm Sát Hạch Lái Xe

và các tổ hợp tuyến tính của chúng là các hàm khác nhau nhưng có cùng chuỗi Taylor tại

Hơn nữa, nếu một hàm

có chuỗi Taylor hội tụ đến chính nó thì tổng của

và bất kỳ hàm nào trong các hàm

hay tổ hợp tuyến tính của hai hàm này có cùng chuỗi Taylor với hàm

. Khi đó nếu ta chỉ biết chuỗi Taylor của

thì ta chưa biết nhiều về

Vậy điều kiện gì để đảm bảo

khi

Thác triển lẻ, tuần hoàn chu kỳ

ta được hàm không liên tục tại

Tiếp tục chuỗi Fourier-sine ta có một số kết quả thú vị sau.

Bài 2.5.56, 57 (trong “Problems in mathematical analysis III”).

Cho dãy

là dãy đơn điệu, hội tụ về

. Chuỗi Fourier-sine

hội tụ đến hàm liên tục khi và chỉ khi

Chú ý: Nếu chỉ quan tâm đến hội tụ thì dùng Định lý Dirichlet ta không cần điều kiện

Bài 2.5.58 (trong “Problems in mathematical analysis III”).

Cho dãy

là dãy đơn điệu, hội tụ về

. Chuỗi Fourier-sine

hội tụ đến hàm bị chặn khi và chỉ khi

(nghĩa là có số

0″ class=”latex” /> để

” bản thân J. Fourier cũng đơn giản cho rằng chuỗi Fourier của hàm liên tục sẽ hội tụ. Phải đến năm 1873 Paul du Bois Reymond mới đưa ra ví dụ một hàm liên tục có chuỗi Fourier phân kỳ tại một vài điểm.

Xem thêm: Bài 58 Tổng Kết Chương 3 Quang Học

Một câu hỏi lại được đặt ra, liệu có cách nào khác để từ các hệ số Fourier của một hàm liên tục, tuần hoàn chu kỳ