ĐỊNH LÍ THALÈS – ĐỊNH LÍ ĐẢO – Học Để Thi

Định lý Tales – Định lý đảo

Xem Thêm : Hướng dẫn cách viết Bản tự kiểm điểm đúng, chuẩn – LuatVietnam

Hệ quả của Định lý Thales

Xem Thêm : Hướng dẫn cách viết Bản tự kiểm điểm đúng, chuẩn – LuatVietnam

Xem Thêm : Hướng dẫn cách viết Bản tự kiểm điểm đúng, chuẩn – LuatVietnam

1. Định lý thalès (talet) trong tam giác:

Xem Thêm : Hướng dẫn cách viết Bản tự kiểm điểm đúng, chuẩn – LuatVietnam

1.1. Tỷ lệ của hai dòng:

Định nghĩa: Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.

1.2. Quy mô phân khúc:

Định nghĩa: Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức :

1.3. Định lý Thales trong tam giác:

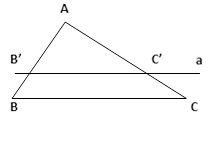
Định lí: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì hai cạnh đó có các đoạn thẳng tỉ lệ.

Xem Thêm : Hướng dẫn cách viết Bản tự kiểm điểm đúng, chuẩn – LuatVietnam

2. Hệ quả của Định lý đảo ngược và Định lý Thales:

Xem Thêm : Hướng dẫn cách viết Bản tự kiểm điểm đúng, chuẩn – LuatVietnam

2.1. Định lýĐảo Thalès:

Định lý: Nếu một đường thẳng cắt hai cạnh của một tam giác và xác định các đoạn thẳng tỉ lệ với hai cạnh đó thì đường thẳng đó song song với cạnh kia của tam giác.

Tam giác abc là

Þ a // bc

Xem Thêm : Hướng dẫn cách viết Bản tự kiểm điểm đúng, chuẩn – LuatVietnam

2.2. Kết quả của định lý Thales:

Kết quả: Nếu một đường thẳng cắt hai cạnh của một tam giác (hoặc cắt bớt phần mở rộng của hai cạnh) và song song với cạnh kia thì tạo thành một tam giác mới có ba cạnh tương ứng bằng ba cạnh của tam giác đã cho .các cạnh tỉ lệ.

Cho tam giác abc có // bc

Bộ sưu tập:

1. là góc xoay. Trên tia X lấy 2 điểm a, b theo thứ tự sao cho oa = 2cm, ab = 3cm. Trên tia oy lấy điểm c có oc = 3cm. Từ điểm b kẻ đường thẳng song song với ac cắt oy tại d. Tính độ dài cd.

2. Δabc là trọng tâm g của tam giác. Vẽ đường thẳng song song với ab qua g, cắt bc tại d. Bằng chứng:

3. Δabc,ab = 7,5cm. Lấy điểm d và .

trên ab

a) Tính da, db

b) Kẻ DHAC tại H, BKAC tại K. Tính tỉ số DH v BK.

c) tức là ak = 4,5cm. Tính hk.

4. là ∆abc. Từ điểm d thuộc cạnh bc kẻ các đường thẳng song song với ab và ac lần lượt cắt ab và ac theo thứ tự e và f. Đếm:

Xem Thêm : Hỗ trợ giải bài 34 trang 123 sgk toán 7 tập 1 – Ngắn gọn và Dễ hiểu

5. là ∆abc. Từ d trên cạnh ab kẻ đường thẳng song song với bc cắt ac tại e. Trên tia đối với tia ca lấy điểm f sao cho cf = db. Gọi m là giao điểm của df và bc. bằng chứng

6. Cho các hình vuông abcd, mbc, điểm n nằm trên tia đối của tia bc sao cho bn = cm. Các đường thẳng dn, dm cắt ab tại e, f theo thứ tự đó.

Bằng chứng: ae2 = eb.ef

7. Đường thẳng đi qua đỉnh a của hình vuông abcd cắt bd, bc, dc lần lượt tại e, k, g. Bằng chứng:

a) ae2 = ek.eg

hai)

8. Có một đường cao cho ∆abc. Trên ah, lấy điểm k, i : ak = ki = ih. vẽ đường thẳng qua i và k ef // bc, mn // bc (e, m ab; f, n ac)

a) Tính

b) nói. đếm?

9. Cho ∆abc, bc = 10cm. Lấy các điểm d, e trên cạnh ab sao cho ad = de = eb. Từ d, e vẽ đường thẳng song song với bc lần lượt cắt cạnh ac tại m, n. Tính dm và en.

10. Hình thang abcd (ab//cd, ab<cd) có hai đường chéo ac và bd cắt nhau tại o. Bằng chứng: oa.od = ob.oc

11. Cho hình thang abcd (ab//cd, ab<cd). Đường thẳng song song với mặt đáy ab cắt các cạnh và các đường chéo ad, bd, ac, bc lần lượt tại các điểm m, n, p, q. Chứng minh: mn = pq.

12. Cho hình thang abcd (ab//cd, ab<cd). Gọi trung điểm của hai đường chéo ac và bd lần lượt là n và m. Bằng chứng:

a) mn // ab

hai)

13. Hình thang abcd (ab//cd, ab<cd) có hai đường chéo ac và bd cắt nhau tại o. Một đường thẳng đi qua o và song song với đáy ab cắt các cạnh ad và bc lần lượt tại m, n. Chứng minh rằng om = on.

14. Cho hình thang abcd (ab//cd,ab<cd). Gọi m l là trung điểm của cd. Gọi i là giao điểm của am và bd, k là giao điểm của bm và ac.

a) Chứng minh: ik // ab.

b) Đường thẳng ik cắt ad và bc lần lượt tại e và f. Chứng minh: ei = ik = kf.

15. Đó là △abc vuông a, đường cao. Vẽ hình vuông dc từ điểm d nằm giữa h và c (e thuộc ac); dk là hình vuông của ac (k thuộc ac). Chứng minh: Đúng // hk

16. Cho tam giác abc, điểm i thuộc cạnh ab, điểm k thuộc cạnh ac. Vẽ im // bk (m thuộc ac) và kn // ci (n thuộc ab). Chứng minh: mn // bc