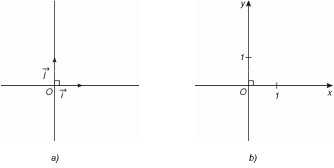
1. Trục và độ dài đại số trên trục
a) Trục tọa độ: Trục tọa độ là đường thẳng xác định gốc tọa độ \(o\) và véc tơ đơn vị \(\vec e\)
b) Tọa độ của một điểm: Với mỗi điểm \(m\) trên trục tọa độ tồn tại một số thực \(k\) sao cho
\(\overrightarrow {om} = k\overrightarrow e \)
Số \(k\) gọi là tọa độ của điểm \(m\) so với trục đã cho.
c) Độ dài đại số: Cho hai điểm \(a,b\) trên trục số, tồn tại một số duy nhất\(a\) sao cho \(\overrightarrow {ab} = a \overrightarrow e \)
\(a\) được gọi là độ dài đại số của vectơ \(\overrightarrow {ab} \), ký hiệu \(a = \overrightarrow {ab} \).
Ghi chú:
– Nếu vectơ \(\overrightarrow {ab} \) cùng hướng với vectơ đơn vị \(\vec e\) của trục thì \(\overline { ab } > 0 \ ), nếu \(\overrightarrow {ab} \) ngược hướng với vectơ đơn vị \(\vec e\), thì \(\overline {ab } <0\ )
– Nếu điểm \(a\) có tọa độ trên trục \(a\) và điểm \(b\) có tọa độ trên trục \(b\)
\(\overline {ab} =b-a\)
2. Hệ tọa độ
a) Định nghĩa: Hệ tọa độ \(\left( {0;\overrightarrow i ;\overrightarrow j } \right)\) gồm hai trục\(\left( { 0 ; \overrightarrow i } \right)\) và \(\left( {0;\overrightarrow j } \right)\) vuông góc với nhau.
Xem Thêm : Đề thi học kì 2 Lớp 3 môn Toán (Có đáp án) năm 2021 – Đề số 2
\(o\) là gốc
\(\left( {0;\overrightarrow i } \right)\) là trục hoành
\(\left( {0;\overrightarrow j } \right)\) là trục tung
\(|\overrightarrow i | = |\overrightarrow j |=1\)
Mặt phẳng được trang bị hệ tọa độ được gọi là mặt phẳng tọa độ
b) Tọa độ vectơ
\(\overrightarrow u = x\overrightarrow i + y\overrightarrow j \leftrightarrow u(x;y)\)
Hai vectơ bằng nhau khi và chỉ khi tọa độ tương ứng bằng nhau
\(\overrightarrow u (x;y);\overrightarrow {u’} (x’;y’)\)
\(\overrightarrow u = \overrightarrow {u’} \leftrightarrow \)\(x = x’\) và \(y = y’\)
c) Toạ độ của một điểm:
Với mỗi điểm \(m\) trong mặt phẳng tọa độ, tọa độ của vectơ \(\overrightarrow {om} \) được gọi là tọa độ của điểm \(m\).
\(\overrightarrow {om} = x\overrightarrow i + y\overrightarrow j \leftrightarrow m(x;y)\)
Xem Thêm : Mô hình 5W1H là gì? Ứng dụng của 5W1H trong Marketing – Epic SEO
d) Mối quan hệ giữa tọa độ của điểm và vectơ:
Cho hai điểm \(a({x_a},{y_a});b({x_b},{y_b})\)
Ta có \(\overrightarrow {ab} ({x_b} – {x_a};{y_b} – {y_a})\)
Tọa độ của vectơ bằng tọa độ của đỉnh trừ đi tọa độ tương ứng của điểm đầu.
3. Tọa độ của tổng, hiệu và phép nhân của các số và vectơ
Cho hai vectơ \(\overrightarrow u ({u_1};{u_2});\overrightarrow v ({v_1};{v_2})\)
Chúng tôi có
\(\eqalign{ & \overrightarrow u + \overrightarrow v = ({u_1} + {v_1};{u_2} + {v_2}) \cr & \overrightarrow u – overrightarrow v = ({u_1} – {v_1};{u_2} – {v_2}) \cr & k\overrightarrow u = (k{u_1};k{u_2}) \cr} \)
4. Tọa độ trung điểm đoạn thẳng và tọa độ trọng tâm tam giác
a) Tọa độ trung điểm: Cho hai điểm\(a({x_a},{y_a});b({x_b},{y_b})\) tọa độ trung điểm\(i({x_i} ; { y_i})\) được tính như sau:
$$\left\{ \ma trận{ {x_i} = {{{x_a} + {x_b}} \ trên 2} \hfill \cr {y_i} = {{{y_a} + {y_b}} \ trên 2} \hfill \cr} \right.$$
b) Tọa độ trọng tâm: tam giác \(abc\) \(a({x_a},{y_a});b({x_b},{y_b) } với các đỉnh \(3\) ) ;c({x_c};{y_c})\). Trọng tâm\(g\) của tam giác có tọa độ:
$$\left\{ \ma trận{ {x_g} = {{{x_a} + {x_b} + {x_c}} \ trên 3} \hfill \cr {y_g} = {{ {y_a} + {y_b} + {y_c}} \hơn 3} \hfill \cr} \right.$$
loigiaihay.com
Nguồn: https://xettuyentrungcap.edu.vn
Danh mục: Hỏi Đáp
