Hình trụ là gì? Công thức tính diện tích và thể tích hình trụ – HOCMAI
Có thể bạn quan tâm
- 3 biện pháp cải tạo đất bạc màu đơn giản hiệu quả chi phí thấp
- Rick roll là gì? Ý nghĩa đúng nhất của từ này – Chanh Tươi
- Thị trường điện tử (Electronic Market, e-market) là gì?
- Lập luận là gì? Các phương pháp lập luận trong văn nghị luận?
- Ý Nghĩa Phim 50 Sắc Thái – 50 Sắc Thái Đen Và 10 Chuyện Có Thể Bạn Chưa Biết
Hình trụ là một dạng hình học không gian thú vị được sử dụng rộng rãi trong cuộc sống hàng ngày. Vậy bạn đã thực sự hiểu các tính chất, công thức tính toán liên quan đến khối hình học quen thuộc này chưa? Cùng hocmai tìm hiểu trong bài viết sau
Tôi. Khái niệm xi lanh
Hình trụ là một không gian hình học (3d) được giới hạn bởi hai đường tròn có đường kính bằng nhau và một hình trụ.
Theo định nghĩa của sách giáo khoa toán lớp 9, hình trụ là:
“Hình trụ là thế giới gồm hình trụ và hai đường tròn bằng nhau, giao tuyến của hình trụ và hai mặt phẳng vuông góc với trục.“
“Hình trụ là một hình tròn được tạo bởi bốn cạnh của một hình chữ nhật khi nó quay quanh đường tâm của nó.”
Nói một cách dễ hiểu hơn, khi xoay hình chữ nhật abcd quanh một cạnh cố định (cạnh ab trong ví dụ bên dưới), ta được một hình trụ:
Để có thể nhận biết hình trụ một cách dễ dàng, bạn có thể dựa vào một số tính chất sau:
- Xi lanh có đế tròn và đường kính bằng nhau
- Bằng nhau khi hai cạnh song song
- Đường nối tâm của hai đáy là trục của hình trụ.
- Đường thẳng cùng độ dài và song song với trục tọa độ gọi là đường sinh của hình trụ.
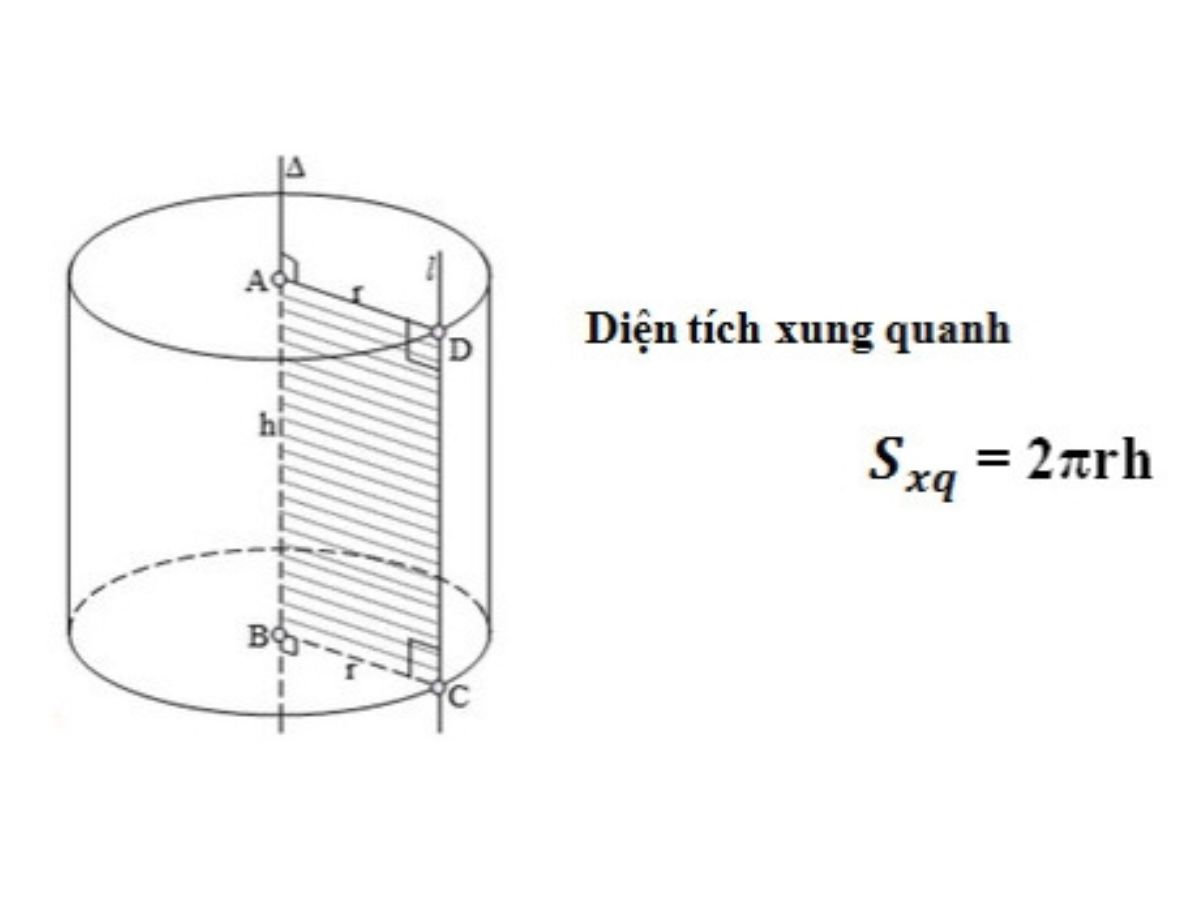
- sxq là diện tích xung quanh hình trụ
- 2πr là chu vi của hình tròn cơ sở (π = 3,14)
- h là chiều cao của hình trụ
- stp là tổng diện tích của đáy
- 2πr^2 Diện tích hai hình tròn đáy (π = 3,14)
- 2πrh là khu vực xung quanh căn cứ
- v là thể tích của hình trụ
- πr² là diện tích đáy
- h là chiều cao
Hai. Công thức và cách tính diện tích hình trụ
Diện tích hình trụ bao gồm diện tích xung quanh và diện tích toàn phần của nó. Sau đây là công thức tính và cách tính cụ thể diện tích các loại hình trụ.
1. Diện tích xung quanh hình trụ
Diện tích xung quanh là chu vi hình trụ, không kể diện tích 2 đáy.
Để tính diện tích xung quanh một hình trụ, chúng ta nhân chu vi của hình tròn đáy với chiều cao. Công thức cụ thể là:
sxq = 2.π.r.h

Ở đâu:
2. Tổng diện tích xi lanh
Xem Thêm : Sức khỏe Môi trường là gì?
Diện tích toàn phần của hình trụ gồm chu vi và diện tích đáy của hình trụ.
Để tính diện tích toàn phần của hình trụ ta cộng diện tích xung quanh hình trụ với diện tích hai đáy. Công thức cụ thể là:
stp = 2.π.r² + 2.π.r.h
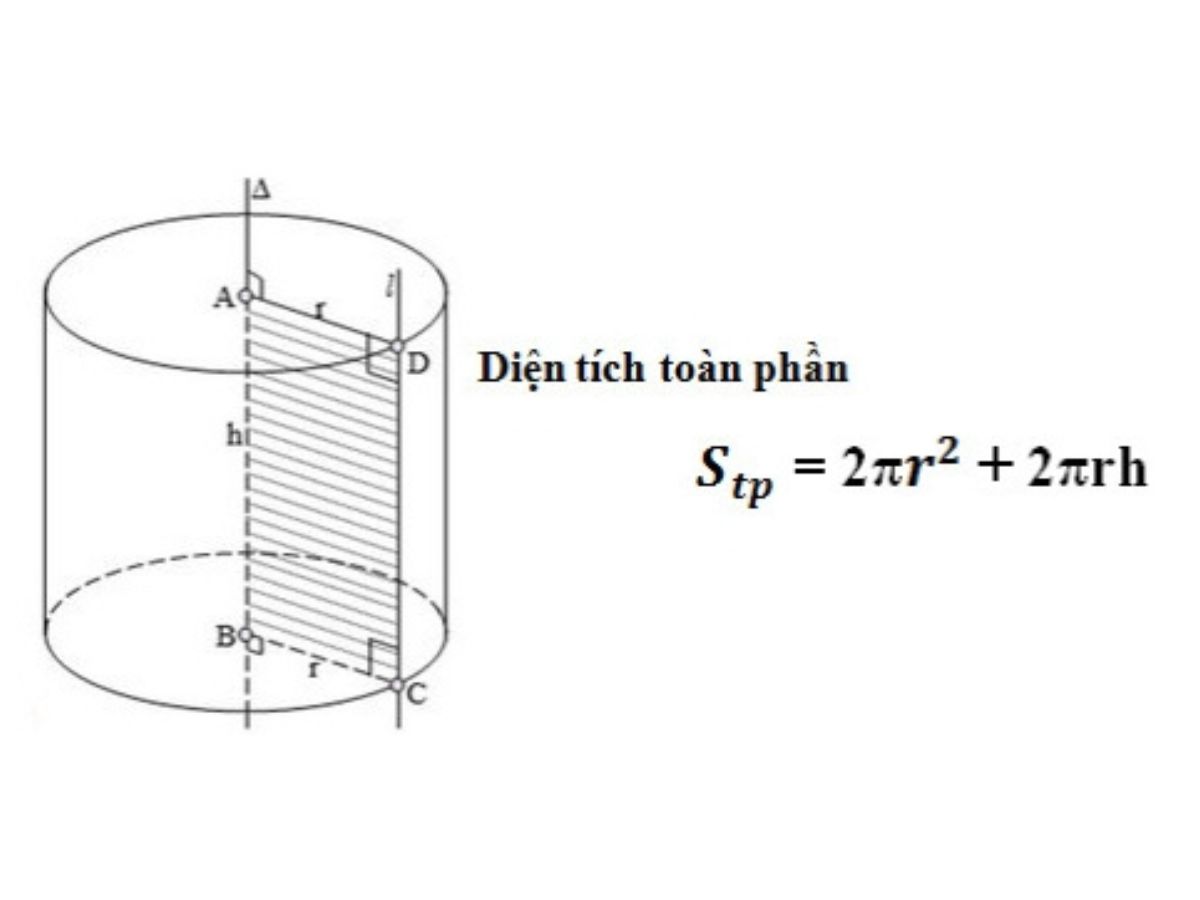
Ở đâu:
3. Ví dụ tính chu vi và diện tích toàn phần của hình trụ
Bài tậpCho một hình trụ, r = 5 cm, h = 10 cm. Tính chu vi và diện tích toàn phần của hình trụ.
Hướng dẫn giải quyết
Diện tích xung quanh hình trụ là:
sxq = 2 * * r * h = 2 * * 5 * 10 = ~ 314 (cm2)
Diện tích toàn phần của hình trụ là:
stp = 2 * π * r ^2* + sxq = 2 * π * 5^2 + 314= ~ 471 cm2
Ba. Thể tích và cách tính thể tích của khối trụ
Thể tích của hình trụ là phần không gian mà hình trụ đó chiếm. Để tính thể tích của hình trụ, bạn cần sử dụng đơn vị khối của khoảng cách (khoảng cách được nâng lên lũy thừa bậc 3).
1. Công thức thể tích xi lanh
Thể tích hình trụ là lượng không gian mà một hình trụ đã cho chiếm. Để tính thể tích của hình trụ, ta nhân diện tích đáy với chiều cao của hình trụ. Cụ thể là:
Xem Thêm : Công chứng chờ là gì? Rủi ro xảy ra khi công chứng chờ | Đất Xuyên Việt Blog
v = .r².h
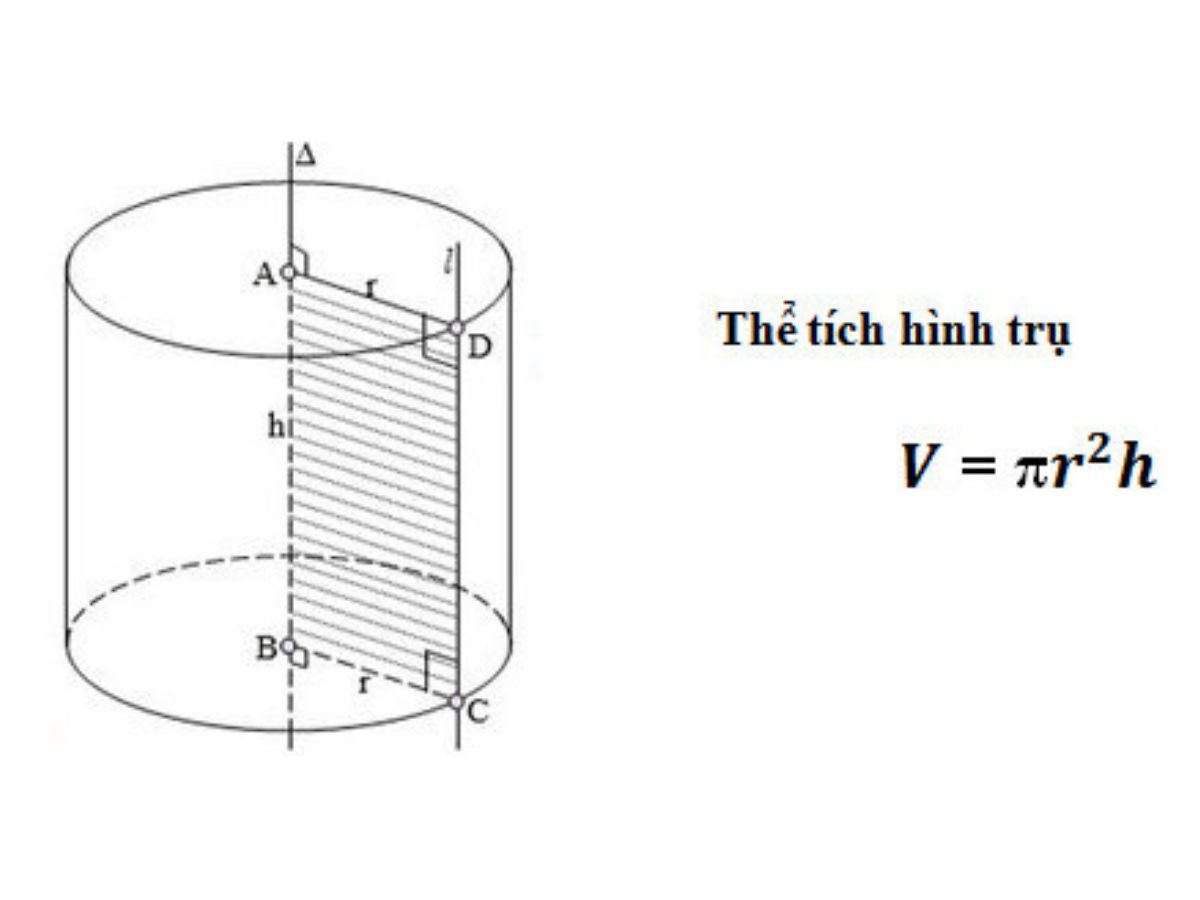
Ở đâu:
2. Ví dụ tính thể tích khối trụ
Bài tậpCho một hình trụ, r = 5 cm, h = 10 cm. Tính thể tích của khối trụ.
Hướng dẫn giải quyết
Thể tích của hình trụ là:
v = *r^2 * h = *5^2 * 10 = ~785 (cm3)
Ba. Ứng dụng của xi lanh trong đời sống hàng ngày
Theo các chuyên gia, so với các hình khối thông thường như hình lập phương, khối cầu thì hình trụ có nhiều đặc điểm nổi bật như khả năng chịu lực tốt, khả năng lưu trữ không gian lớn. Do đó, trong cuộc sống hàng ngày, bạn sẽ bắt gặp rất nhiều ứng dụng của xi lanh. Trong số đó, lon nước ngọt với thiết kế hình trụ là ứng dụng phổ biến nhất của bạn.
Nhờ khả năng chịu tải cực tốt, xi lanh được mô phỏng qua nhiều hình dạng kết cấu khác nhau như ống khói, ống dẫn nước, cột,…
Một số bài viết có thể bạn quan tâm:
Cách tính diện tích hình tròn, chu vi hình tròn
Diện tích hình bình hành, chu vi hình bình hành
Cách tính diện tích hình thang, chu vi hình thang
hocmai hy vọng bài viết này có thể giúp các em hiểu rõ hơn về hình trụ và những kiến thức liên quan đến môn hình học không gian thú vị này. Truy cập hoctot.hocmai.vn để biết thêm những kiến thức Toán học tương tự và đừng bỏ lỡ những bài viết mới nhất của chúng tôi!
Nguồn: https://xettuyentrungcap.edu.vn
Danh mục: Hỏi Đáp