[Lớp 10] Công thức tính độ dài đoạn thẳng đầy đủ & bài tập áp dụng

Kiến thức về hệ tọa độ Oxyz trong không gian được coi là rất quen thuộc trong chương trình thpt, từ khi chúng ta được tiếp cận với hình học Oxy. Vậy nói về tính chất và quan hệ giữa các điểm trong không gian có khác gì hình học phẳng không? Câu hỏi này sẽ giải đáp một phần câu hỏi đó bằng công thức tính độ dài đoạn thẳng. voh education sẽ chia sẻ công thức tính độ dài đoạn thẳng và đưa ra ví dụ để các bạn tham khảo.

1. Tổng quát hóa hệ tọa độ trong không gian để sử dụng trong việc xây dựng công thức tính độ dài đoạn thẳng

Các kiến ​​thức toán học về hệ tọa độ trước câu hỏi này chỉ áp dụng cho mặt phẳng, tiếp theo chúng ta sẽ tìm hiểu về hệ tọa độ Oxy. Tuy nhiên, thực tế không thể mô tả các đối tượng trong không gian bằng hình học phẳng. Vì vậy, để thể hiện rõ ràng các tính chất của khối đa diện, ta cần thành lập hệ trục tọa độ oxyz.

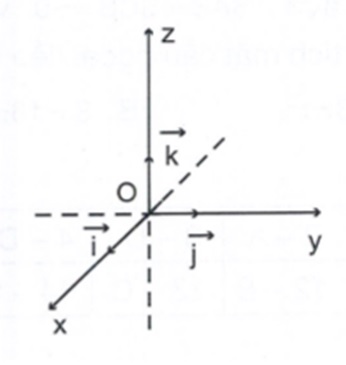
Trong không gian, hệ gồm ba trục tọa độ x’ox, y’oy, z’oz đôi một vuông góc với nhau được gọi là hệ trục tọa độ thẳng đứng không gian.

• Điểm o gọi là gốc tọa độ.
• Trục bò: Trục ngang.
• oy axis: trục tung.
• oz axis: trục chiều cao.

Mặt phẳng chứa hai trục tọa độ được gọi là mặt phẳng tọa độ, được biểu diễn bởi (oxy), (oyz), và (ozx).

Ba vectơ đơn vị ox, oy và oz trên ba trục (1;0;0), (0;1;0) và (0;0,1) được gọi tương ứng.



» Xem thêm:Hệ tọa độ không gian và các công thức quan trọng

2. Mô tả tọa độ của một điểm để xây dựng công thức tính độ dài đoạn thẳng

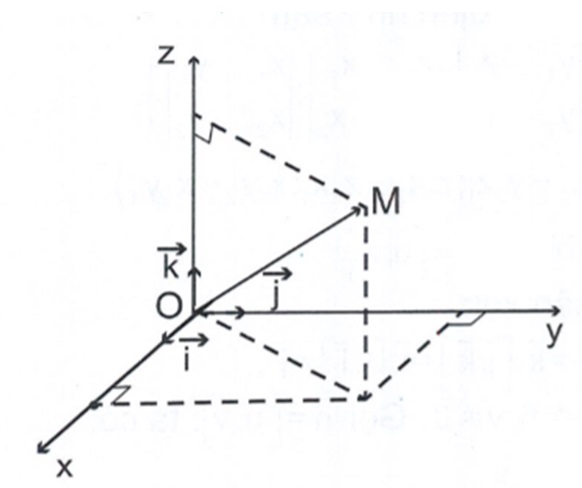
Với mỗi điểm m, tồn tại một bộ ba (x; y; z) duy nhất sao cho . Ta gọi bộ ba (x;y;z) là tọa độ của điểm m.

Ký hiệu: m(x; y; z) hoặc m = (x; y; z).

Do đó ⇔ m(x; y; z).

Nếu tọa độ của điểm m là (x;y;z) thì x, y, z lần lượt được gọi là tọa độ, tọa độ và độ cao của điểm m.

Nhận xét:

Điểm m trên các trục tọa độ ox, oy, oz:

m ∈ ox ⇔ m(x; 0; 0); m oy ⇔ m(0; y; 0)

Điểm m thuộc mặt phẳng (oxy), z = 0, thuộc mặt phẳng (oyz), x = 0, thuộc mặt phẳng (oxz), y = 0.

Biểu diễn tọa độ của điểm:

Cho bốn điểm a(xa; ya; za), b(xb; yb; zb), c(xc; yc; zc), d(xd; yd; zd)

Ta có:

• = (xb – xa; yb – ya; zb – za)

• ab =

• Trung điểm i của ab có tọa độ:

• Tôi

• Trọng tâm g của tam giác abc có tọa độ:

• gam

• Tỷ số điểm n của ab theo k:

• = n

Xem Thêm : Trọn Bộ Quy Tắc Đánh Vần Tiếng Anh Chuẩn Nhất Cho Người Mới



*Ví dụ

• = ⇔ = (3; -1; -3) ⇔ m (3; -1; -3)

• = ⇔ = (2; -1; 0) ⇔ n (2; -1; 0)

• = = p

3. Tọa độ mô tả véc tơ dùng để xây dựng công thức tính độ dài đoạn thẳng

Trong không gian oxyz, với mỗi vectơ, tồn tại một bộ ba duy nhất (x; y; z) sao cho . Ta gọi bộ ba (x; y; z) là toạ độ của vectơ. Ký hiệu: hoặc.

Biểu thức tọa độ cho các phép toán vectơ:

Với hai vectơ , , ta có:

• = (x1 + x2; y1 + y2; z1 + z2)

• = (x1 – x2; y1 – y2; z1 – z2)

• = (kx1; ky1; kz1), k ∈ r

Kích thước véc tơ:

• =

Tích vô hướng của hai vectơ:

• = x1x2 + y1y2 + z1z2

Góc giữa hai vectơ:

• cosin = =

0

Đặc biệt:

Hai vectơ bằng nhau

⇔

Hai vectơ cùng phương khi và chỉ khi , k ∈ r

• ⇔ = 0 ⇔ x1x2 + y1y2 + z1z2 = 0

*Ví dụ

• Cho hai vectơ (1; -3; 4), (-2; 3; 5)

• Kích thước vectơ:

• Tích vô hướng của hai vectơ:

• Góc giữa hai vectơ:

4. Công thức tính độ dài đoạn thẳng trong không gian oxyz

Xem Thêm : Khối D gồm những ngành nào? Danh sách các trường khối D HOT

Công thức tính lặp lại độ dài của một đoạn thẳng trong hình học phẳng:

Cho vecto = (u1; u2)

• Kích thước của vectơ

Cho hai điểm a (xa; ya), b (xb; yb)

• = (xb – xa; yb – ya)

• ab = =

Công thức tính độ dài đoạn thẳng trong không gian:

• Cho vectơ (x1; x2; x3)

Kích thước véc tơ:

•

*Ví dụ minh họa

•

Kích thước véc tơ

•

Hai điểm

•

• ab =

Cho hai điểm a(1;2;-3), b(2;-2;1)

•

•

5. lớp 10 ứng dụng công thức tính độ dài đoạn thẳng

bài 1: Trong không gian của hệ tọa độ oxyz, cho các vectơ: = (1; 2; -3), = (2; 1; 1), , = (3 ; – mười ) .Véc tơ nào có độ dài lớn nhất ?

A.

*phương thức

Để tính độ dài của vectơ, chúng ta sử dụng công thức sau:

• Đối với vectơ

• Kích thước của vectơ

*Cách khắc phục

Véc tơ: