Bài 3: Con lắc đơn – Hoc247.vn
Hôm nay chúng ta tiếp tục bài 3 Con lắc đơn. Vậy con lắc là gì?
Bạn thực sự đã học về con lắc đơn ở lớp 10. Nhưng hôm nay chúng ta sẽ đào sâu và xem xét các sự kiện chính về con lắc để chuẩn bị cho kỳ thi. Đây là thpt.
Xem Thêm : Soạn bài Chị em Thúy Kiều (trích Truyện Kiều) | Soạn văn 9 hay nhất
I. Cấu trúcgồm một sợi dây mềm, nhẹ, không đàn hồi và một quả cầu khối lượng m.
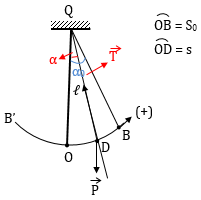
II. Phương trình động lực học của con lắc đơn  Theo định luật II Niuton \(\overrightarrow{T} + \overrightarrow{P} = m\overrightarrow{a} (*)\) Chiếu (*) lên phương trình tiếp tuyến: \(P_t = ma_t\) Với \(\left\{\begin{matrix} P_t = -P\sin \alpha = – mg \sin \alpha \\ a_t = s” \hspace{3,5cm} \end{matrix}\right.\) \(\Rightarrow -g \sin \alpha = s” \ (1)\) * Nếu \(\mathbf{\alpha _0 \leq 10^0}\) \(\Rightarrow \sin \alpha \approx \alpha = \frac{s}{\ell}\) \(\Rightarrow -g.\frac{s}{\ell} = s” \Leftrightarrow s” = -\frac{g}{\ell}.s\) Đặt \(\omega ^2 = \frac{g}{\ell} \Rightarrow s” = -\omega ^2.s \ (2)\) Nghiệm của (2) có dạng \(s = S_0.\cos (\omega t + \varphi )\) Vậy dao động bé \((\alpha _0 \leq 10^0)\) của con lắc đơn là dao động điều hòa với chu kỳ \(T = \frac{2 \pi}{\omega } = 2 \pi \sqrt{\frac{\ell}{g}}\) * Các phương trình của con lắc đơn dao động điều hòa + Phương trình li độ: Dài: \(s = S_0 \cos (\omega t + \varphi )\) Góc: \(\alpha = \alpha _0 \cos (\omega t + \varphi )\) \((S_0 = \alpha _0.\ell;\ s = \alpha .\ell)\) + Phương trình vận tốc: \(v = s’ = -\omega S_0.\sin (\omega t + \varphi )\) + Phương trình gia tốc: \(a = v’ = s”\) \(\Rightarrow a = -\omega ^2.S_0. \cos (\omega t + \varphi ) = -\omega ^2s\) * Năng lượng con lắc đơn dao động điều hòa • Wđ \(=\frac{1}{2}mv^2 = \frac{1}{2}m\omega ^2S_{0}^{2}. \sin^2 (\omega t + \varphi )\) • Wt \(=\frac{1}{2}m\omega ^2 s^2= \frac{1}{2}m\omega ^2S_{0}^{2}. \cos ^2 (\omega t + \varphi )\) • W = Wđ + Wt = \(\frac{1}{2}mv^2 + \frac{1}{2}m \omega ^2 s^2\) = hằng số Nhận xét: Đối với con lắc đơn dao động điều hòa thì bài tập tương tự con lắc lò xo nếu thay \(s = x; S_0 = A; m\omega ^2 = k\) * Xét năng lượng – vận tốc – lực căng dây trong trường hợp tổng quát + Năng lượng: • Wđ \(=\frac{1}{2}mv^2\) • \(W_t = ph = mg\ell (1-\cos \alpha )\) ⇒ W = Wđ + Wt = \(\frac{1}{2}mv^2 + mg \ell (1 – \cos \alpha )\) (hằng số) W = Wđ max = \(\frac{1}{2}mv_{max}^{2}\) (VTCB) \(W = W_{t \ max} = mg\ell (1 – \cos \alpha _0)\) + Vận tốc: Ta có: Wđ + Wt = Wt max \(\Rightarrow \frac{1}{2}mv^2 + mg\ell (1-\cos \alpha ) = mg \ell (1-\cos \alpha _0)\) \(\Rightarrow v^2 = 2g\ell (\cos \alpha – \cos \alpha _0)\) • \(|v|_{max} = \sqrt{2g \ell (1-\cos \alpha _0)}\) (VTCB) • \(|v|_{min} = 0\) (VT biên) + Lực căng dây: Chiếu (*) lên phương sợi dây, chiều dương hướng tâm: T – Pn = maht Với \(\left\{\begin{matrix} P_n = P.\cos = mg \cos \alpha \hspace{1,2cm}\\ a_{ht} = \frac{v^2}{\ell } = 2g(\cos \alpha – \cos \alpha _0) \end{matrix}\right.\) \(\Rightarrow T = mg\cos \alpha + m.2g(\cos \alpha – \cos \alpha _0)\) \(\Rightarrow T = mg(3 \cos \alpha – 2\cos \alpha _0)\) \(\cdot \ T_{max} = mg(3 – 2 \cos \alpha _0) > P\) \(\cdot \ T_{min} = mg\cos \alpha _0 < P\)
Theo định luật II Niuton \(\overrightarrow{T} + \overrightarrow{P} = m\overrightarrow{a} (*)\) Chiếu (*) lên phương trình tiếp tuyến: \(P_t = ma_t\) Với \(\left\{\begin{matrix} P_t = -P\sin \alpha = – mg \sin \alpha \\ a_t = s” \hspace{3,5cm} \end{matrix}\right.\) \(\Rightarrow -g \sin \alpha = s” \ (1)\) * Nếu \(\mathbf{\alpha _0 \leq 10^0}\) \(\Rightarrow \sin \alpha \approx \alpha = \frac{s}{\ell}\) \(\Rightarrow -g.\frac{s}{\ell} = s” \Leftrightarrow s” = -\frac{g}{\ell}.s\) Đặt \(\omega ^2 = \frac{g}{\ell} \Rightarrow s” = -\omega ^2.s \ (2)\) Nghiệm của (2) có dạng \(s = S_0.\cos (\omega t + \varphi )\) Vậy dao động bé \((\alpha _0 \leq 10^0)\) của con lắc đơn là dao động điều hòa với chu kỳ \(T = \frac{2 \pi}{\omega } = 2 \pi \sqrt{\frac{\ell}{g}}\) * Các phương trình của con lắc đơn dao động điều hòa + Phương trình li độ: Dài: \(s = S_0 \cos (\omega t + \varphi )\) Góc: \(\alpha = \alpha _0 \cos (\omega t + \varphi )\) \((S_0 = \alpha _0.\ell;\ s = \alpha .\ell)\) + Phương trình vận tốc: \(v = s’ = -\omega S_0.\sin (\omega t + \varphi )\) + Phương trình gia tốc: \(a = v’ = s”\) \(\Rightarrow a = -\omega ^2.S_0. \cos (\omega t + \varphi ) = -\omega ^2s\) * Năng lượng con lắc đơn dao động điều hòa • Wđ \(=\frac{1}{2}mv^2 = \frac{1}{2}m\omega ^2S_{0}^{2}. \sin^2 (\omega t + \varphi )\) • Wt \(=\frac{1}{2}m\omega ^2 s^2= \frac{1}{2}m\omega ^2S_{0}^{2}. \cos ^2 (\omega t + \varphi )\) • W = Wđ + Wt = \(\frac{1}{2}mv^2 + \frac{1}{2}m \omega ^2 s^2\) = hằng số Nhận xét: Đối với con lắc đơn dao động điều hòa thì bài tập tương tự con lắc lò xo nếu thay \(s = x; S_0 = A; m\omega ^2 = k\) * Xét năng lượng – vận tốc – lực căng dây trong trường hợp tổng quát + Năng lượng: • Wđ \(=\frac{1}{2}mv^2\) • \(W_t = ph = mg\ell (1-\cos \alpha )\) ⇒ W = Wđ + Wt = \(\frac{1}{2}mv^2 + mg \ell (1 – \cos \alpha )\) (hằng số) W = Wđ max = \(\frac{1}{2}mv_{max}^{2}\) (VTCB) \(W = W_{t \ max} = mg\ell (1 – \cos \alpha _0)\) + Vận tốc: Ta có: Wđ + Wt = Wt max \(\Rightarrow \frac{1}{2}mv^2 + mg\ell (1-\cos \alpha ) = mg \ell (1-\cos \alpha _0)\) \(\Rightarrow v^2 = 2g\ell (\cos \alpha – \cos \alpha _0)\) • \(|v|_{max} = \sqrt{2g \ell (1-\cos \alpha _0)}\) (VTCB) • \(|v|_{min} = 0\) (VT biên) + Lực căng dây: Chiếu (*) lên phương sợi dây, chiều dương hướng tâm: T – Pn = maht Với \(\left\{\begin{matrix} P_n = P.\cos = mg \cos \alpha \hspace{1,2cm}\\ a_{ht} = \frac{v^2}{\ell } = 2g(\cos \alpha – \cos \alpha _0) \end{matrix}\right.\) \(\Rightarrow T = mg\cos \alpha + m.2g(\cos \alpha – \cos \alpha _0)\) \(\Rightarrow T = mg(3 \cos \alpha – 2\cos \alpha _0)\) \(\cdot \ T_{max} = mg(3 – 2 \cos \alpha _0) > P\) \(\cdot \ T_{min} = mg\cos \alpha _0 < P\)
Nguồn: https://xettuyentrungcap.edu.vn
Danh mục: Hỏi Đáp