Luyện tập 2: Giải bài 39 40 41 42 trang 124 sgk Toán 7 tập 1

Bài tập thực hành 2 §5. Trường hợp đồng dư thứ ba của tam giác góc-cạnh-góc (g.c.g), Chương 2 – Hình tam giác, SGK Toán 7 I. Nội dung giải bài 39 40 41 Trang 42 124 SGK Toán 7 Tập 1 tổng hợp các công thức, lý thuyết và phương pháp giải phần hình học trong SGK toán giúp học sinh học tốt môn Toán lớp 7.

Lý thuyết

1. Vẽ tam giác biết một cạnh và hai góc kề nhau

Để vẽ được tam giác abc, tổng độ của hai góc cho trước phải nhỏ hơn \({180^0}\)

2. Trường hợp cạnh-góc đều

Hai tam giác bằng nhau nếu một cạnh và hai góc kề bù của tam giác này bằng một cạnh và hai góc kề bù của tam giác kia.

3. hậu quả

Hậu quả 1:

Các tam giác vuông bằng nhau nếu các cạnh và các góc nhọn kề của tam giác vuông này bằng các cạnh và các góc nhọn kề của tam giác vuông kia.

Hậu quả 2:

Các tam giác vuông bằng nhau nếu cạnh huyền và góc nhọn của tam giác vuông này bằng cạnh huyền và góc nhọn của tam giác vuông kia.

Dưới đây là hướng dẫn giải bài trang 39, 40, 41, 42, 124 SGK Toán 7 Tập 1. Các em hãy đọc kỹ bài đầu tiên trước khi giải bài nhé!

Bài tập 2

giaibaisgk.com giới thiệu đến các bạn trọn bộ phương pháp giải bài tập chi tiết Bài 7, bài 39 40 41, bài 42 trang 124 Tập 7, tập 1 §5 SGK Toán. Chương 3 Trường hợp tương đương thứ ba của tam giác góc-cạnh-góc (g.c.g) – tam giác để các bạn tham khảo. Chi tiết lời giải của từng bài tập xem bên dưới:

1. Giải bài 39 trang 124 SGK Toán 7 Tập 1

Trên mỗi hình 105, 106, 107, 108 có tam giác vuông nào bằng nhau không? Tại sao?

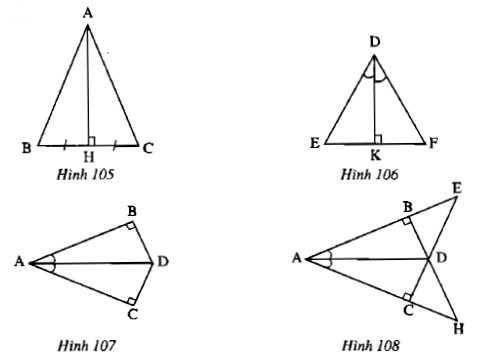
Giải pháp:

– Hình 105:Xét hai tam giác vuông $ahb$ và $ahc$ trong đó:

$\left.\begin{matrix} hb = hc (gt)\ edge\, ha\, chung \end{matrix}\right\}$

⇒ $\delta hba = \delta hca$ (hai góc vuông)

– Hình 106: Hai tam giác vuông $ked$ và $kfd$ có:

$\left.\begin{matrix} edge\, kd \,General \\ \widehat{edk} = \widehat{fdk} (gt) \end{matrix} Đến\}$

⇒ $\delta ked = \delta kfd$ (góc vuông – góc nhọn)

– Hình 107:Xét hai tam giác vuông $bad$ và $cad$:

$\left.\begin{matrix} \widehat{bad} = \widehat{cad} (gt) \\ cạnh\, cạnh huyền\, ad\, chung \ end {ma trận}\right\}$

⇒ $\delta xấu = \delta cad$ (góc cường điệu).

– Hình 108: Theo tổng ba góc trong định lý tam giác ta có:

\(\eqalign{ & \widehat {abd} + \widehat {bda} + \widehat {dab} = {180^0} \cr & \widehat {acd} + \widehat {cda} + \widehat {dac} = {180^0} \cr} \)

Xem Thêm : Soạn bài Lẽ ghét thương (Nguyễn Đình Chiểu) – VietJack.com

Ngược lại ta có:

\(\eqalign{ & \widehat {dab} = \widehat {dac}\,\,\,(gt) \cr & \widehat {abd} = widehat {acd} = {90^0} \cr} \)

Phải là \(\widehat {bda} = \widehat {cda}\)

Xét \(Δabd\) và \(Δacd\) có:

\(\widehat {dab} = \widehat {dac}\,\,\,(gt)\)

\(ad\) cạnh chung

\(\widehat {bda} = \widehat {cda}\) (cmt)

Suy ra: \(Δabd=Δacd\) (g.c.g)

Suy ra: \(bd=cd\) (hai cạnh tương ứng)

\(ab=ac\) (hai cạnh tương ứng)

Xét \(Δdbe\) và \(Δdch\)

\( \widehat {ebd} = \widehat {hcd} = {90^0} \)

\(bd=cd\) (cmt)

\(\widehat {bde} = \widehat {cdh}\) (đối diện)

Suy ra: \(Δdbe=Δdch\) (g.c.g)

Xét \(Δabh\) và \(Δace\)

\(\widehat a\) trung bình

\(ab=ac\) (cmt)

\(\widehat {abh} = \widehat {ace} = {90^0}\)

Suy ra: \(Δabh=Δace \) (g.c.g)

2. Giải bài 40 trang 124 sgk toán 7 tập 1

Đối với tam giác $abc (ab \neq ac)$, tia $ax$ đi qua trung điểm $m$ của $bc$. Vẽ $be$ và $cf$ vuông góc với $ax (e \in ax, f \in ax)$. So sánh độ dài của $be$ và $cf$.

Giải pháp:

Ta có $be // cf$ (cũng vuông góc với ax)

Suy ra $\widehat{ebm}$ = $\widehat{fcm}$ (hai góc so le trong)

Xét hai tam giác vuông $ebm$ và $fcm$:

Xem Thêm : Hàm IF trong Excel: Cách sử dụng có ví dụ đơn giản dễ hiểu

$\left.\begin{matrix} \widehat{ebm} = \widehat{fcm} (cmt)\\ edge\, mb = mc \,(gt) \end {ma trận}\right\}$

⇒ $\delta ebm = \delta fcm$ (góc cường điệu)

Suy ra: $be = cf$(hai cạnh tương ứng).

3. Giải bài 41 trang 124 sgk toán 7 tập 1

Tam giác $abc$. Tia phân giác của hai góc $b$ và $c$ cắt nhau tại $i$. Vẽ $id \perp ab (d \in ab), nghĩa là $$\perp$ bc (e $\in$ bc), nếu $\perp$ ac (f $\in$ ac ). Chứng minh rằng $id = ie = if$.

Giải pháp:

– Xét hai tam giác vuông $ifc$ và $iec$:

Cường điệu $ic$ phổ biến

$\widehat{fci}$ = $\widehat{eci}$ (ci là tia phân giác của góc c)

Do đó $\delta$ ifc = $\delta$ iec (góc cường điệu)

Suy ra $if = ie$(1) (hai cạnh tương ứng)

– Xét hai tam giác vuông $ibe$ và $ibd$:

Cường điệu $bd$ phổ biến

$\widehat{ibe}$ = $\widehat{ibd}$ (bi là tia phân giác của góc b).

Vậy $\delta$ ibe = $\delta$ ibd (góc cạnh huyền)

suy ra $ie = id$ (2) (hai cạnh tương ứng)

Suy ra từ (1) và (2) mà $id = ie = if$ (dpcm)

4. Giải bài 42 trang 124 sgk toán 7 tập 1

Đối với tam giác $abc$ ta có $\widehat{a}$ = $90^0$ (h.109). Vẽ ah vuông góc với bc (h $\in$ bc). Cạnh chung của tam giác ahc và bac là ac và góc chung là $\widehat{c}$, $\widehat{ahc}$ = $\widehat{bac}$ = $90^0$, nhưng hai tam giác Ý nghĩa không bằng nhau.

Tại sao trường hợp góc-cạnh-góc không thể được sử dụng ở đây để nhận được $\delta$ ahc = $\delta$ bac?

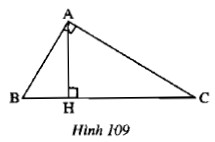
Giải pháp:

Theo đề bài, ta thấy cạnh $ac$ kề với góc $c$ và góc $bac$ của tam giác $abc$, nhưng không kề với góc $c$ và góc $ahc$ nên góc – bên Ví dụ – c. có thể kết luận rằng $\delta ahc = \delta bac$ là.

Trước:

• Giải bài 33 34 35 tr.123 SGK Toán 7 tập 1
• Bài tập 1: Giải trang 36 37 38 trang 123 124 SGK Toán 7 Tập 1

Tiếp theo:

• Bài tập về ba tam giác đồng dạng: Giải bài 43 44 45 trang 125 SGK Toán 7 Tập 1

Xem thêm:

• Câu hỏi khác 7
• Học tốt vật lý lớp 7
• Học tốt môn sinh học lớp 7
• Học tốt ngữ văn lớp 7
• Điểm tốt môn lịch sử lớp 7
• Học tốt môn địa lý lớp 7
• Học tốt tiếng Anh lớp 7
• Học tốt môn tiếng Anh lớp 7 thí điểm
• Học tốt môn tin học lớp 7
• Học chăm chỉ gdcd lớp 7

Chúc các em thành công trong việc ôn tập SGK Toán 7 Tập 39 40 41 Trang 42 124 SGK Toán 7 Tập 1!

“Bài tập nào khó, đã có giabaisgk.com”