Góc giữa 2 vecto trong không gian: Lý thuyết, bài tập & tài liệu
Có thể bạn quan tâm
- Vũng Tàu có đặc sản gì? 15 đặc sản Vũng Tàu mua làm quà
- Lý thuyết: Những ứng dụng của tin học trang 53 SGK Tin học 10
- JD, JP và CV là viết tắt của gì? Tìm hiểu về JD, JP … – Lưu sơn Hotel
- Google Drive là gì? Có những tính năng gì? Cách sử dụng Google
- Các Dạng Bài Tập Câu Hỏi đuôi (Tag Question) đầy đủ Nhất
Trong hình học không gian, tính góc giữa hai vectơ trong không gian là một bài toán khó trong chương trình toán lớp 12 dựa trên nhiều kiến thức khác nhau liên quan đến mặt phẳng và thiết diện. Hiểu được sự khó khăn khi làm dạng bài này, verbalearn sẽ giúp các bạn hiểu rõ hơn trong các bài viết sau.
Xác định góc giữa hai vectơ trong không gian
Góc giữa hai vectơ trong không gian có cùng định nghĩa với góc giữa hai vectơ trong mặt phẳng. Chúng ta có hai định lý như sau:
- Nếu có một vectơ 0 thì góc là không xác định (có thể nói là góc bằng 0)
- Hai vectơ không bằng 0, tiếp tục quay về cùng một gốc để tính toán
Tính chất góc giữa hai vecto
Gọi là góc giữa hai vectơ bất kỳ trong không gian $ alpha $. Chúng tôi có các thuộc tính sau:
- $ alpha = {0 ^ 0} $ khi hai vectơ cùng hướng
- $ alpha = {90 ^ 0} $ khi hai vectơ vuông góc
- $ alpha = {180 ^ 0} $ khi hai vectơ ngược hướng nhau
li>
Công thức tính góc giữa hai vectơ
Áp dụng công thức tính góc giữa hai vectơ có thể giúp bạn tính nhanh các bài toán cơ bản. Dưới đây là công thức chung cho một vectơ không gian. Để tính góc giữa hai vectơ, hãy sử dụng công thức sau để tính cosin của góc, sau đó chuyển nó thành số đo khi bài toán yêu cầu.
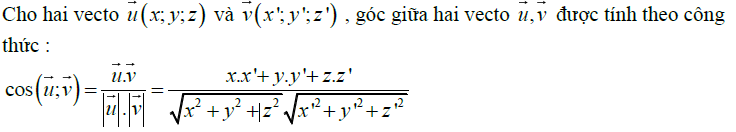
Lưu ý
Góc giữa hai vectơ nằm trong khoảng sau: $ { rm {[}} {0 ^ 0}; {180 ^ 0} { rm {]}} $
Tích của hai vectơ trong không gian
Xem Thêm : 1 chén cơm bao nhiêu calo? Ăn cơm nhiều có mập không, nên chọn
Tích số chấm của hai vectơ trong không gian là một kiến thức quan trọng. Sử dụng công thức tích dấu chấm, không chỉ có thể tính được cosin của một góc mà còn có thể xác định được nhiều yếu tố khác.
1. Góc giữa hai vectơ chung
2. Tích số chấm của hai vectơ trong không gian
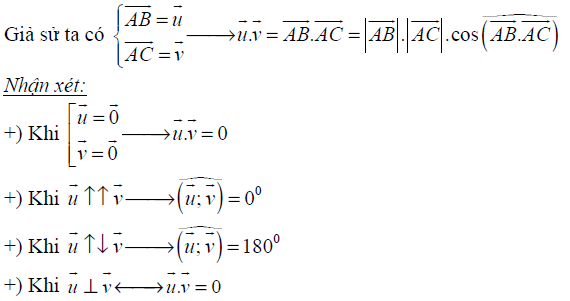
3. Ví dụ học tập
Bài toán 1: Tính góc tạo bởi các vectơ phụ của tứ diện đều.
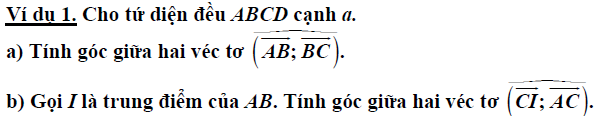
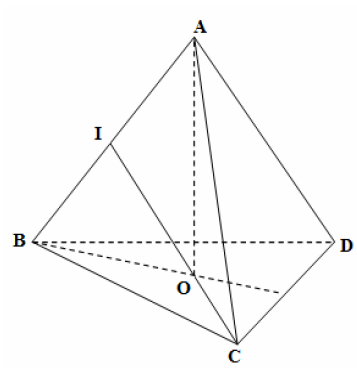


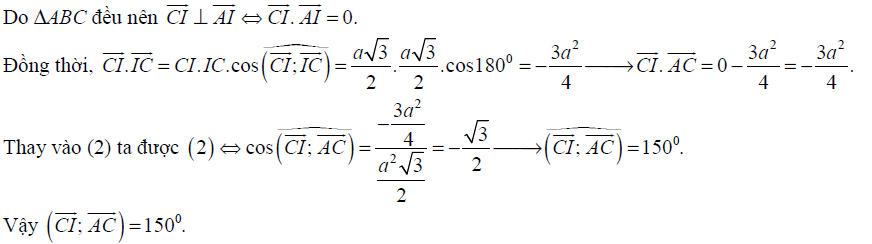
Trên đây là bài toán cơ bản nhất về tính góc giữa hai vectơ. Khi gặp bài toán này cần lưu ý đến các tính chất của tứ diện đều để tránh bỏ sót dữ kiện. Tiếp theo chúng ta đến với một bài toán tính góc giữa hai vectơ, bài toán đưa ra là một hình chóp có bao nhiêu yếu tố thẳng đứng.


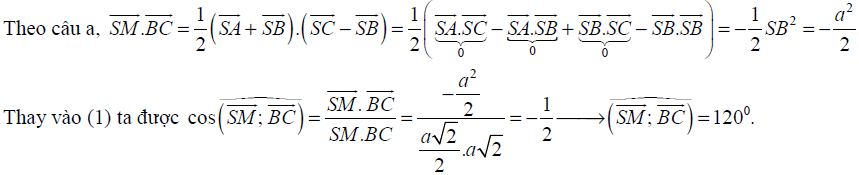
Sử dụng casio để tính góc giữa hai vectơ
Vì môn toán đã được thay đổi thành các kỳ thi trắc nghiệm, nên bạn phải sử dụng máy tính CASIO để giải các bài toán. Không chỉ đại số, mà ngay cả hình học, sử dụng máy tính cầm tay vẫn có giá trị. Lưu ý để thành thạo casio trước hết bạn phải nắm vững lý thuyết, để không làm mất đi bản chất của môn học.
1. Các lệnh liên quan đến định dạng thẻ đầu vào casio
- Lệnh đăng nhập khi làm toán vectơ: chế độ 8
- Đầu vào tham số vectơ: chế độ 8 1 1
- Tính tích số chấm của hai vectơ: vectơ shift 5 7 vectorob
- Tính tích của hai vectơ: vectoa x vectob
- Lệnh giá trị tuyệt đối: shift hyp
- Lệnh cường độ vectơ: shift hyp
- Nghiệm của bất phương trình: Chế độ 7
- Lệnh giải phương trình: shift giải
Tìm hiểu về các lệnh nhập casio liên quan đến vectơ. Để tính góc bằng casio, cách nhanh nhất là bạn thực hiện lại theo ví dụ sau.
2. Ví dụ minh họa
Câu 1: Sử dụng tọa độ để tính góc giữa hai vectơ đã cho
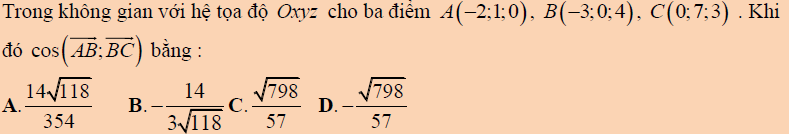
Xem Thêm : Google api key là gì ? Hướng dẫn lấy google api key mới nhất 2020 – Lamweb.vn
Nhập hai vectơ $ ( overrightarrow {ab}; overrightarrow {bc}) $ vào máy tính:

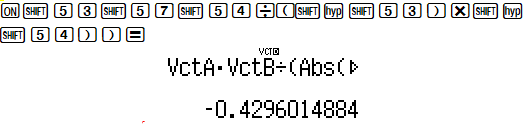
→ câu trả lời là b
Câu thứ hai : Tìm điều kiện của các tham số để góc giữa hai vectơ thỏa mãn yêu cầu cho trước
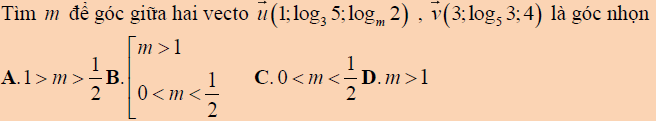
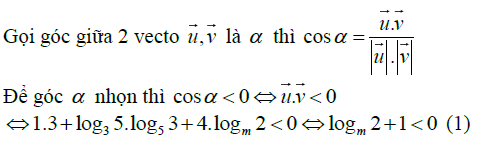
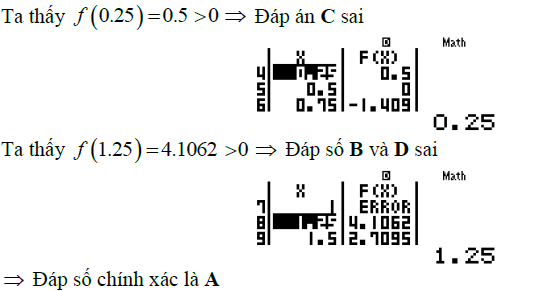
Câu thứ ba : tìm tham số m thỏa mãn số đo góc
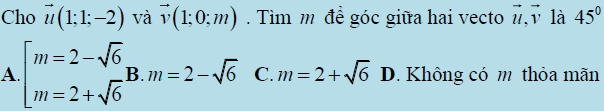
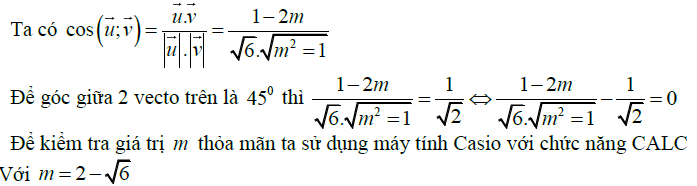
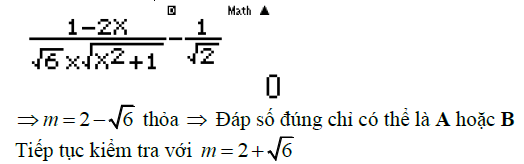
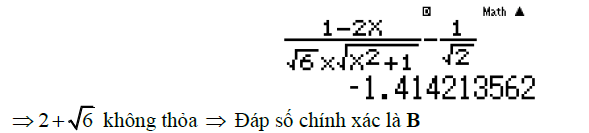
Trên đây là toàn bộ về góc giữa hai vectơ trong không gian và một số cách tính. Ngoài kỹ năng sử dụng máy tính, để thành thạo dạng bài tập này, học sinh cần nắm được các tính chất của vectơ không gian, các công thức lượng giác cơ bản. Cuối cùng, verbalearn chúc các bạn may mắn và học chắc các dạng bài này nhé.
Nguồn: https://xettuyentrungcap.edu.vn
Danh mục: Hỏi Đáp



